
Department of Physics and Astronomy
209 South 33rd Street
University of Pennsylvania
Philadelphia, PA 19104-6396
Theoretical Condensed Matter Physics
Our research interests center on problems in condensed matter theory.
We are currently exploring problems in liquid crystals, foams, soft self-assembly, and biological
physics.
Materials Geometry
We are fortunate that soft matter systems are large enough so that we can
treat them geometrically. Geometry is powerful because it is
scale-invarient. Once a principle of organization is understood in one
system, the structure can be translated to different scales,
materials, and interactions.
For instance, minimal surfaces have a long history of lying in the interface between
Physics and Mathematics. Their use has had somewhat of a
revival due to the ever increasing complexity of lyotropic
phases of matter. Block copolymers and amphiphiles form
structures that resemble doubly-
and triply-periodic minimal surfaces. This
is no surprise: because physics
problems can be posed as extremal problems and because the
mean curvature is the lowest-degree, rotationally-invariant
scalar, minimal surfaces arise as solutions. However, nonlinearities
should play an important role as the lengthscales of the structures
become comparable to molecular sizes.
Likewise, hard sphere systems are pure: their physics is governed solely by entropic depletion interaction with the only adjustable
parameter being the volume fraction. Despite their simplicity, many details of
the freezing transition are not understood. We are interested in the rigorous viability of the
so-called random-close-packed state. Through geometric methods we are probing this
state via analytic and numerical approaches. We study the equation of state via modifications
to the virial expansion. We are also interested in the packing of long, stiff and semi-stiff
polymers in the presence of entropic depletors.
Liquid Crystals
The theory of liquid crystals and liquid crystalline polymers
runs the gamut from the rheology of complex fluids to the esoterica of
homotopy and topological defects. All aspects of theory are
intimately influenced and connected
with experiment. This places liquid crystal physics in an exciting position:
it is driven by both theory and experiment and by both the abstract
and the applied.
Specifically, chiral molecules are ubiquitous in nature and exhibit many liquid crystal
phases.
They are extensively studied by biologists, chemists and biophysicists.
There is still much theoretical work to be done on the wealth of
experimental data.
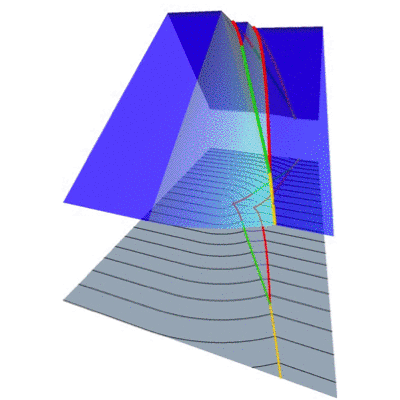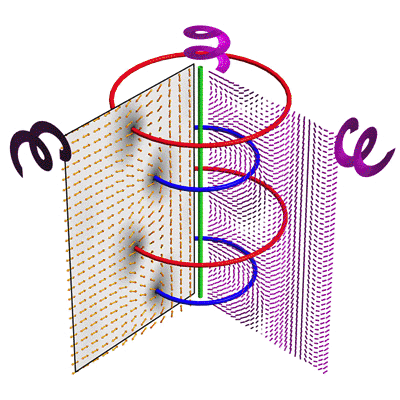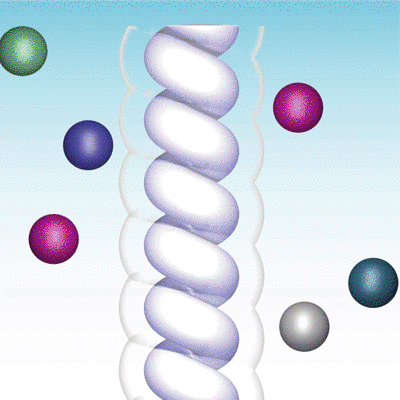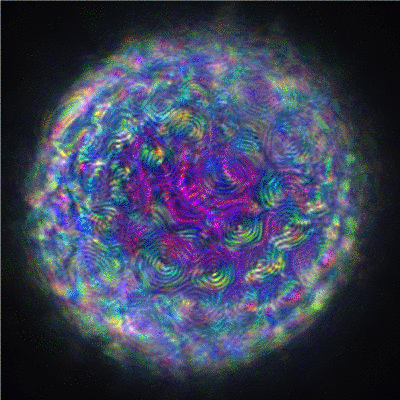
Smectic liquid crystals as well as columnar liquid crystals
have the analogue of the Meissner phase in superconductors, in which
chirality is excluded from the bulk (just as the magnetic field is
expelled in a superconductor). The constraints imposed by topology
and geometry can screen out chirality as well. We are studying the nonlinear
elasticity of these phases through exact solutions and geometric principles.
Using methods of topology we are classifying the structure and
interactions of topological defects in these and more complex systems.
This work has been or is supported, in part, through the Simons
Foundation, the Charles E. Kaufman Foundation a supporting organization
of The Pittsburgh Foundation, the ACS Petroleum Research Fund, the Advanced
Functional Fabrics of America Grant W15QKN-16-3-0001, and the
National Science Foundation Through Grants DMR-9732963, INT-9910017,
DMR-0102459, DMR-0129804, DMR-0520020, DMR-0547230, CMMI-0900468,
DMR-1120901, DMR-1262047, EFRI-1331583, and DMR-1720530.
Last modified 29 June 2021

