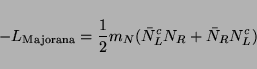Next: Models of neutrino mass
Up: THEORETICAL FRAMEWORK
Previous: THEORETICAL FRAMEWORK
Weyl, Dirac, and Majorana neutrinos
A Weyl two-component spinor is a left (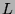 )-handed1 particle state,
)-handed1 particle state, 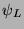 , which is necessarily associated by CPT
with a right (
, which is necessarily associated by CPT
with a right (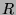 )-handed antiparticle state2
)-handed antiparticle state2 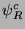 . One refers to active (or ordinary) neutrinos
as left-handed neutrinos
which transform as
. One refers to active (or ordinary) neutrinos
as left-handed neutrinos
which transform as 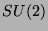 doublets with a charged lepton
partner. They therefore have normal weak interactions, as do their right-handed
anti-lepton partners,
doublets with a charged lepton
partner. They therefore have normal weak interactions, as do their right-handed
anti-lepton partners,
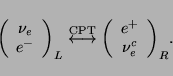 |
(1) |
Sterile3 neutrinos are 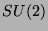 -singlet neutrinos, which can be added to the
standard model and are predicted in most extensions. They have
no ordinary weak interactions except those induced by mixing with active
neutrinos. It is usually convenient to define the
-singlet neutrinos, which can be added to the
standard model and are predicted in most extensions. They have
no ordinary weak interactions except those induced by mixing with active
neutrinos. It is usually convenient to define the 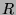 state as the
particle and the related
state as the
particle and the related 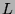 anti-state as the antiparticle.
anti-state as the antiparticle.
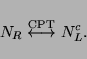 |
(2) |
(Sterile neutrinos will sometimes also be denoted 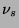 .)
.)
Mass terms describe transitions between right (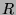 )
and left (
)
and left (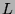 )-handed states.
A Dirac mass term, which conserves lepton number, involves transitions
between two distinct Weyl neutrinos
)-handed states.
A Dirac mass term, which conserves lepton number, involves transitions
between two distinct Weyl neutrinos
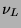 and
and 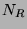 :
:
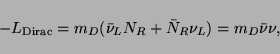 |
(3) |
where the Dirac field is defined as
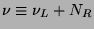 . Thus a
Dirac neutrino has four components
. Thus a
Dirac neutrino has four components
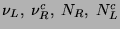 ,
and the mass term allows a conserved lepton number
,
and the mass term allows a conserved lepton number
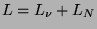 . This and other types of mass terms can easily be generalized
to three or more families, in which case the masses become matrices.
The charged current transitions then involve
a leptonic mixing matrix (analogous to the
Cabibbo-Kobayashi-Maskawa (CKM) quark mixing matrix), which
can lead to neutrino oscillations between the light neutrinos.
. This and other types of mass terms can easily be generalized
to three or more families, in which case the masses become matrices.
The charged current transitions then involve
a leptonic mixing matrix (analogous to the
Cabibbo-Kobayashi-Maskawa (CKM) quark mixing matrix), which
can lead to neutrino oscillations between the light neutrinos.
For an ordinary Dirac neutrino
the 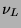 is active
and the
is active
and the 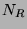 is
sterile.
The transition is
is
sterile.
The transition is
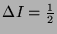 ,
where
,
where 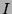 is the weak isospin. The mass requires
is the weak isospin. The mass requires 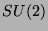 breaking and
is generated by a Yukawa coupling
breaking and
is generated by a Yukawa coupling
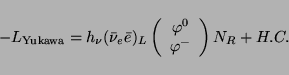 |
(4) |
One has
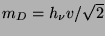 ,
where the vacuum expectation value (VEV) of
the Higgs doublet is
,
where the vacuum expectation value (VEV) of
the Higgs doublet is
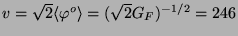 GeV,
and
GeV,
and 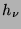 is the Yukawa coupling.
A Dirac mass is just like the quark and charged lepton masses, but
that leads to the question of why it is so small: one requires
is the Yukawa coupling.
A Dirac mass is just like the quark and charged lepton masses, but
that leads to the question of why it is so small: one requires
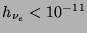 to have
to have 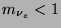 eV.
eV.
A Majorana mass, which violates lepton number by two units
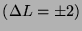 , makes use of the right-handed antineutrino,
, makes use of the right-handed antineutrino,
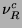 , rather than a separate Weyl neutrino. It is a transition
from an antineutrino into a neutrino. Equivalently, it can be viewed
as the creation or annihilation of two neutrinos, and if present
it can therefore lead to neutrinoless double beta decay.
The form of a Majorana mass term is
, rather than a separate Weyl neutrino. It is a transition
from an antineutrino into a neutrino. Equivalently, it can be viewed
as the creation or annihilation of two neutrinos, and if present
it can therefore lead to neutrinoless double beta decay.
The form of a Majorana mass term is
where
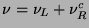 is a self-conjugate two-component state
satisfying
is a self-conjugate two-component state
satisfying
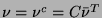 , where
, where 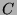 is the
charge conjugation matrix. If
is the
charge conjugation matrix. If 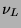 is active then
is active then
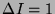 and
and 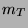 must be generated by either an elementary Higgs
triplet or by an effective operator involving two Higgs doublets
arranged to transform as a triplet.
must be generated by either an elementary Higgs
triplet or by an effective operator involving two Higgs doublets
arranged to transform as a triplet.
One can also have a Majorana
mass term
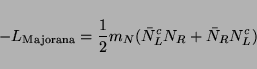 |
(6) |
for a sterile neutrino. This has 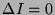 and thus
can be generated by the VEV of a
Higgs singlet4.
and thus
can be generated by the VEV of a
Higgs singlet4.



Next: Models of neutrino mass
Up: THEORETICAL FRAMEWORK
Previous: THEORETICAL FRAMEWORK
Paul Langacker
2001-09-27
![]() )-handed1 particle state,
)-handed1 particle state, ![]() , which is necessarily associated by CPT
with a right (
, which is necessarily associated by CPT
with a right (![]() )-handed antiparticle state2
)-handed antiparticle state2 ![]() . One refers to active (or ordinary) neutrinos
as left-handed neutrinos
which transform as
. One refers to active (or ordinary) neutrinos
as left-handed neutrinos
which transform as ![]() doublets with a charged lepton
partner. They therefore have normal weak interactions, as do their right-handed
anti-lepton partners,
doublets with a charged lepton
partner. They therefore have normal weak interactions, as do their right-handed
anti-lepton partners,
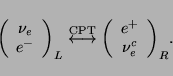
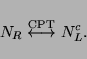
![]() )
and left (
)
and left (![]() )-handed states.
A Dirac mass term, which conserves lepton number, involves transitions
between two distinct Weyl neutrinos
)-handed states.
A Dirac mass term, which conserves lepton number, involves transitions
between two distinct Weyl neutrinos
![]() and
and ![]() :
:
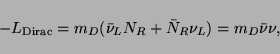
![]() is active
and the
is active
and the ![]() is
sterile.
The transition is
is
sterile.
The transition is
![]() ,
where
,
where ![]() is the weak isospin. The mass requires
is the weak isospin. The mass requires ![]() breaking and
is generated by a Yukawa coupling
breaking and
is generated by a Yukawa coupling
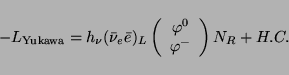
![]() , makes use of the right-handed antineutrino,
, makes use of the right-handed antineutrino,
![]() , rather than a separate Weyl neutrino. It is a transition
from an antineutrino into a neutrino. Equivalently, it can be viewed
as the creation or annihilation of two neutrinos, and if present
it can therefore lead to neutrinoless double beta decay.
The form of a Majorana mass term is
, rather than a separate Weyl neutrino. It is a transition
from an antineutrino into a neutrino. Equivalently, it can be viewed
as the creation or annihilation of two neutrinos, and if present
it can therefore lead to neutrinoless double beta decay.
The form of a Majorana mass term is