Former Postdoc
PhD, University of Colorado at Boulder, 2007
BA, The Colorado College, 1999
CV
Current research interests: foams, liquid crystals
Research techniques: x-ray diffraction, polarized light microscopy, atomic force microscopy, dielectric spectroscopy, particle image velocimetry, image analysis

Rheology of foams:
Christopher D. Jones, Kerstin Nordstrom, DJ Durian
Rheology is the study of flow. Foams are materials that flow in an interesting way. We wish to characterize the stress/strain relationships found in many foams, and to pursue this interest we have constructed the following apparatus:

We have a tall column
(approx. 120 cm by 10 cm by 2.5 cm), in which we have a
pressure driven foam flow, as denoted with the black
arrows, initiated with a gas bubbling into soapy water from
below. The front and back faces of the channel are acrylic
sheet, which is very slippery to the foam - there’s no
distortion in flow or bubble shape due to these surfaces.
The sides of the apparatus can either be “sticky” (sand
paper) or “slippery” (bare acrylic). With the sticky sides,
we see a “no slip” condition - almost no bubbles flow at
the surface of the wall, but within just a few bubble
diameters flow is not constrained.
The call out image in the figure above is one frame from a
video of the flowing foam, where the average bubble
diameter is 4mm, which has been consistent for us at
relatively low flow rates. This image is cut off on the
right at the center of the channel.
By measuring the depth the foam depresses the water (due to
its weight), and the liquid fraction (obtained by measuring
resistance of foam with brass electrodes) of the foam for
the full length of the column, we can use a simple force
balance equation to obtain a driving pressure, which we can
then relate directly to the stress the foam feels between
the driving pressure and the no-slip sides. This is shown
below, where x is the distance from the middle of the
channel, and L is the length of the channel of foam.
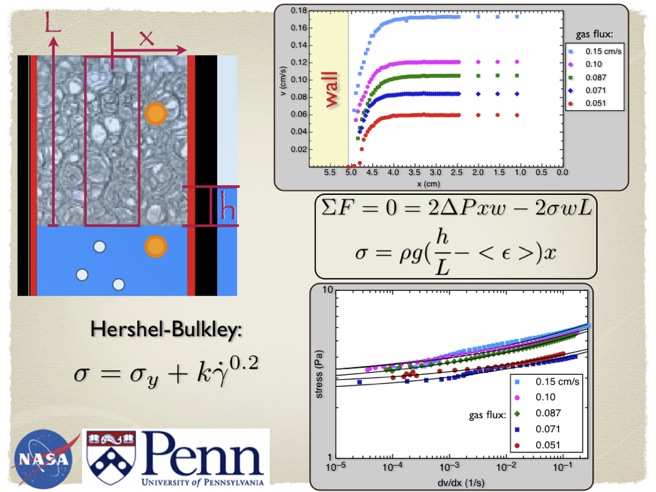
In the top-right plot above,
we show the velocity profile at several flow rates.
Velocity profiles are obtained via particle image
velocimetry. The x-axis goes from the center of the cell,
at x equals zero, to the sandpaper at x equals 5.08cm. With
all this information - depression height h and average
liquid fraction <ε>, as well as the velocity profile
and channel dimensions, we have all the pieces we need to
look into the stress/strain relationship for the foams
we’re investigating, which are shown in the bottom-right
plot.
Coarsening dynamics of 2d
foams on a curved surface:
Christopher D.
Jones,
Jennifer
Rieser,
Adam Roth, DJ Durian
The evolution of 2d foams is a study has enjoyed broad
interest both from experimental and theoretical sides. In
1951, von Neumann’s law for 2d coarsening on a planar
surface was derived [1]. This law interestingly showed that
a bubble with 6 neighbors will not change in size over
time, while bubbles with more neighbors (larger bubbles)
increase in size, and bubbles with fewer neighbors (smaller
bubbles) decrease in size.
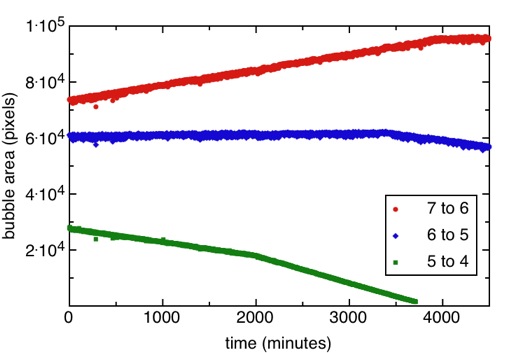
We have developed a
planar-geometry apparatus, that maintains a constant
pressure even as excess solution drains out, that allows us
to experimentally probe dry 2d foams and confirm von
Neumann’s law. Work along these lines has been done before,
especially by Stavans [2], but we have attempted to develop
a system that continuously drains early in the experiment,
becomes a very stable 2d foam during the experiment, and
allows us to follow bubble size versus number of neighbors
over long periods of time. An example of a data set is
shown above, with the inset indicating the number of
neighbors the plotted bubble had before and after a
topological change. This experiment is useful background
for our next step, explained below.
Forty years after von Neumann, Avron and Levine were able
to generalize this law to curved surfaces [3]. This result
showed that when the surface curvature is positive (such as
a bowl), then for a certain size bubble with less than 6
neighbors the bubble will not change size over time. A
bubble with 6 or more neighbors on a positively curved
surface will always increase in size. The case of
negatively curved surfaces (such as a saddle) gives the
result that at less than 6 neighbors a bubble will always
shrink, and with more than 6 neighbors the bubble will
maintain it’s size for only certain sizes, but will
otherwise grow.
This result has not yet been tested experimentally. To
pursue this, we have developed an apparatus of two nested
domes (positive curvature), with differing sizes which
accommodate a constant spacing between them at all points
on the hemisphere. We fill the gap between the two domes
with a foam, and watch the foam coarsen over time. We use a
solution of soapy water with glycerine (the glycerine slows
the drainage of the fluid in the films between bubbles), so
that the primary coarsening mechanism is diffusion of gas
between neighboring bubbles. The gas diffusion is driven by
a pressure differential between two bubbles of different
size and film curvature.

With this apparatus we will
be able to determine coarsening statistics of an individual
bubble’s size, its number of neighbors, and the number of
bubbles in the system, all with respect to time. In doing
so we will be able to establish an experimental response to
the previous theoretical work.
[1] J. von Neumann,
Metal
Interfaces (American Society for Metals, Cleveland,
1952) p. 108.
[2] J. Stavans, Physica A 194, 307 (1993).
[3] J.E. Avron and D. Levine,
Physical Review
Letters 69, 208 (1992).